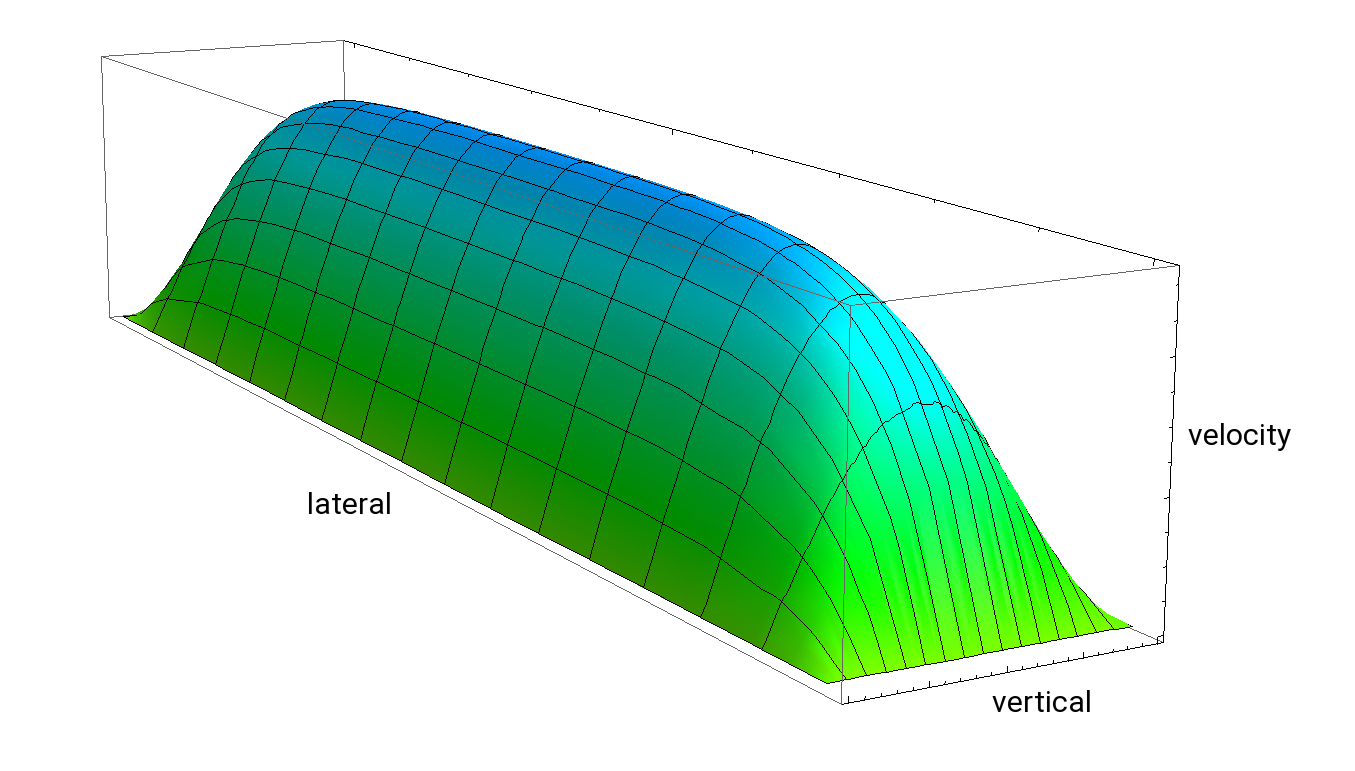
Durchflussraten und -profile in Mikro- und Mesokanälen
Reibung tritt bei Relativbewegungen zwischen festen Körpern, zwischen Fluiden in einem Rohr und dessen Wänden, aber auch fern von Grenzen innerhalb strömender Fluide zwischen Schichten gleicher Geschwindigkeit (Lamellen) auf. Dies hat tiefgreifende Auswirkungen auf das Verhalten des Fluids. Die Strömung in einem Rohr oder einem Kanal kann turbulent oder laminar sein. Dies hängt von der Kanalgröße, der Strömungsgeschwindigkeit und den Eigenschaften der Flüssigkeit ab. Das heißt: Je größer der Kanal, je höher die Strömungsgeschwindigkeit und je niedriger die Viskosität, desto eher entwickelt die Strömung Turbulenzen, die durch die Reynoldszahl (Re) beschrieben werden:
Re = ū ρ L / η
mit der (mittleren) Strömungsgeschwindigkeit ū, der Kanallänge L, der Dichte (ρ) und der dynamischen Viskosität (η) des Fluids. Die charakteristische Dimension ist die Länge, die das Gesamtverhalten des Fluids bestimmt - in unserem Fall kann es die laterale oder vertikale Kanalgröße sein. Re setzt die Strömungsimpulsdichte ū ⋅ ρ (Trägheit) in Beziehung zur Viskosität. Turbulenz beginnt bei Re >2000 ... 3000, eine Zahl, die in Mikrokanälen glücklicherweise kaum erreichbar ist, da L und ρ sehr klein sind.
Daher ist die Strömung in unserem Fall laminar und die Reibung dominiert die Strömungseigenschaften. Die Reibung hat glättende Eigenschaften, scharfe Kanten im Geschwindigkeitsfeld vx(x, y, z) werden sehr schnell abgerundet. Die Viskosität ist die makroskopische Konsequenz der Reibung. Die Diffusion in Flüssigkeiten führt zur Mittelung der Scherkräfte und Minimierung der Gradienten. Allerdings ist es an den Kanalwänden nicht der Fall, da sie stationär sind, also sich a priori nicht bewegen. a priori.
Melden Sie sich zu unserem Newsletter an!
Diese Seite wird regelmäßig mit neuen technischen und Anwendungshinweisen sowie Hintergrundinformationen zu Mikrofluidik, Hydrodynamik aktualisiert. Abonnieren Sie unseren Newsletter, um frühzeitig über Veröffentlichung neuer Beiträge zu erfahren.