Druckbasierte und volumenbasierte Strömungskontrolle in der Mikrofluidik
Spritzen- und Peristaltikpumpen gehören seit Jahrzehnten in die biologischen und chemischen Labore. So war es nachvollziehbar, dass diese für den Einsatz in mikrofluidischen Setups bevorzugt wurden. Die beiden Pumpen basieren auf der volumengesteuerten Strömungskontrolle und haben aus hydrodynamischer Sicht eine Reihe von Nachteilen, wodurch deren Einsatz für Mikrosysteme eher ungünstig wird.
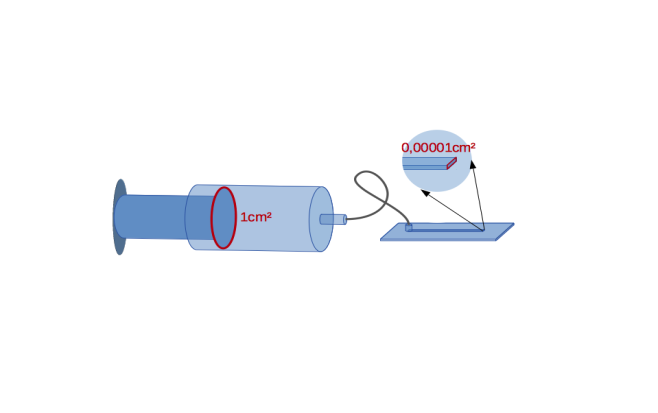
So weisen Spritzenpumpen erhebliche Limitationen in puncto des verfügbaren Flüssigkeitsvolumens auf. Wird eine Spritze mit einer Querschnittsfläche von A = 1 cm2 an einen typischen Mikrokanal von 10×100μm=0,00001xA angeschlossen, ergibt sich eine 100.000-fache Erhöhung der Strömungsgeschwindigkeit im Mikrokanal. Zwar kann ggf. dieser Nachteil durch den Einsatz von kommerziell verfügbaren hochpräzisen Spritzenpumpen überwunden werden, es bleiben jedoch weitere Schwierigkeiten, beispielsweise das Nachfüllen der Spritze während des Experiments, das gezwungenermaßen hierzu unterbrochen werden muss.
Durchflusssensoren und druckbasierte Strömungskontrolle in der Mikrofluidik
Beim Einsatz der druckbasierten Strömungskontrolle in der Mikrofluidik arbeitet man mit Druck, nicht mit volumetrischen Durchflussraten. In einigen Fällen ist es jedoch notwendig oder von Vorteil, die volumetrische Flussrate im Mikrokanal zu kennen. Beispielsweise bei der Realisierung eines vorgegebenen Protokolls für die Zellkultur, Stöchiometrie im Mikrokanal oder einfach zur Überwachung des Verbrauchs von wertvollen Reagenzien. In solchen Situationen kann die Flussrate im Kanal auf unterschiedlichen Wegen bestimmt werden. In der Regel kann man sie berechnen, indem man die Tröpfchen bei bestimmten Druckwerten wiegt und so das System kalibriert. Dies ist die genaueste Methode, sie ist aber auch etwas umständlich. Eine gute Alternative hierzu sind kommerziell verfügbare Durchflusssensoren.
The available flow meters in the market are usually integrated upstream of the microchannel. However, the measured flow rate is not precisely equivalent to the actual volumetric flow rate, since the method is indirect, e.g. based on the temperature or Coriolis force. It makes the calibration before use mandatory. [/text_output][text_output]
Methods of Flow Control
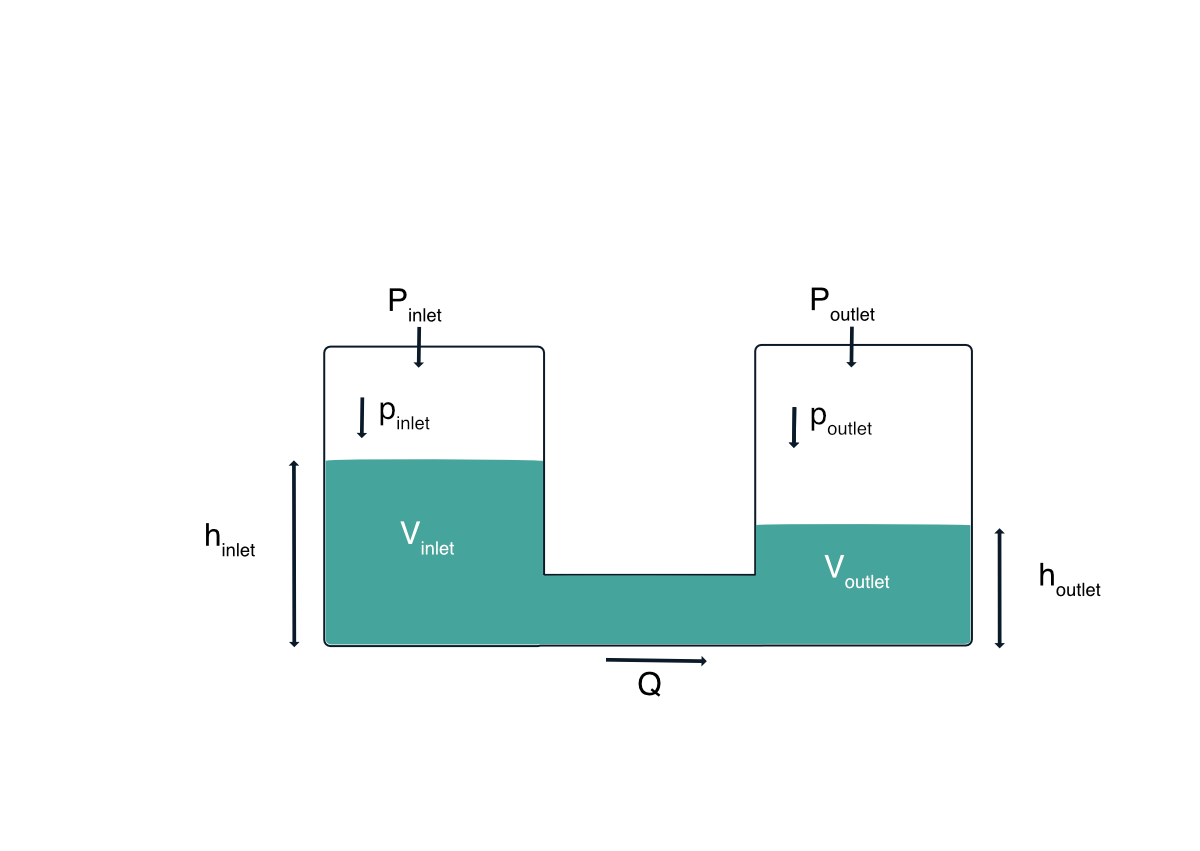
Pressure and flow rate are the main physical parameters which describe flow in microfluidic channels and devices. They are not independent from each other, but related through the flow resistance depending on the channel design and fluid properties quite similar to voltage and current in electrical circuits.
Pressure is defined as force per area and we distinguish hydraulic and pneumatic pressure. These quantities are studied in the fields of Hydraulics and Pneumatics and all together in Hydrodynamics. Hydraulic pressure describes the exerted pressure transmitted by an incompressible medium as a liquid onto an immersed object or a boundary, e. g. water on biological cells or oil phase droplets in multi-phase fluids.
Pneumatischer und hydrostatischer Druck
Unsere Atmosphäre übt Druck auf alle Oberflächen aus. Flüssigkeiten können dies ebenfalls tun. Im Falle der Atmosphäre drückt das Gewicht des gesamten Gases oben aufgrund der Schwerkraft nach unten und erzeugt einen isotropen Druck, der auf Meereshöhe eine ziemlich beeindruckende Größenordnung erreichen kann, die ungefähr dem Druck einer Masse von 1 kg auf 1 cm2entspricht. Flüssigkeiten haben jedoch eine viel höhere Dichte als Luft, etwa das 1000-fache, und mit der Tiefe steigt der Druck viel schneller an. Der Druck einer Flüssigkeit in Abhängigkeit von deren Gewicht wird als hydrostatischer Druck bezeichnet.
Veranschaulichen wir das Ganze anhand eines Zylinders (oder einer anderen Form) auf einer ebenen Fläche Z. Der Zylinder mit einer bestimmten Masse und Gravitationskraft F übt einen Druck p auf die untere Grenzfläche mit gegebener Fläche aus: p=F / A. Dies gilt für feste, flüssige und gasförmige Stoffe gleichermaßen. Ersetzt man den Kraftterm mit den Materialeigenschaften einer Flüssigkeit, z. B. Wasser, und den geometrischen Eigenschaften des hypothetischen Zylinders, so ergibt sich ein hydrostatischer Druck von p = h ·ρ · g,, wobei h Höhe der Flüssigkeitssäule ist, ρ (“rho”) the liquid density and g the gravitational acceleration. Thus, the hydrostatic pressure does not depend on the size of the cross-sectional area of the liquid column, but only on the height of the liquid column and the density of the liquid. In fact, the hydrostatic pressure is also indifferent to the shape of the hypothetical column.
[text_output]Melden Sie sich zu unserem Newsletter an!
We regularly update this page with new technical and application notes as well as background information on Microfluidics, Hydrodynamics and more. If you want to stay updated, please subscribe.[/text_output]