Pressure-driven and Volume-driven Flow Control in Microfluidics
Since decades syringe and peristaltic pumps belong to biological and chemical laboratories. Thus, it was comprehensible that they were the first choice for the use with microfluidic devices, i.e. at a microscale. Still, in the hydrodynamical view both instruments for the volume-driven flow control have a number of bottlenecks which make them not favourable for the use at a microscale.
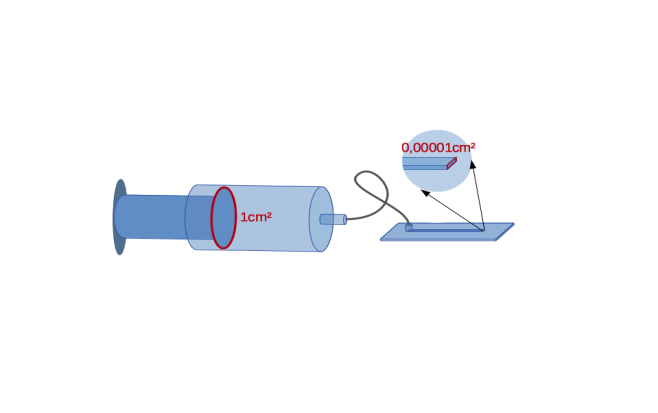
For instance, syringe pumps have considerable limits on the side of the liquid column. If a syringe with a cross-sectional area of A = 1 cm2 is connected to a typical microchannel of 10×100μm=0.00001xA cross-section, this results in a 100,000-fold amplification of the flow velocity in the microchannel. Probably, this disadvantage can be overcome by usage of highly precise syringe pumps in the market, but still there will be more difficulties, such as refilling the volume during the experiment, which has necessarily to be interrupted for it.
Flow Meters and Pressure-driven Flow Control in Microfluidics
When working with pressure-driven flow control systems in Microfluidics, we are working with pressure, not with volumetric flow rates. However, in some cases it is necessary or helpful to know the volumetric flow rate of the fluid in the microchannel. For example, in order to follow a specific protocol for a cell culture, stoichiometry in the microchannel or just to monitor the consumption of precious reagents. In such cases there are different approaches to determine the flow rate in the channel. In general, you can calculate it by weighing the droplets at specific pressure values and thus calibrate the system. This is the most precise method, however, cumbersome. Or you can use commercially available flow meters.
The available flow meters in the market are usually integrated upstream of the microchannel. However, the measured flow rate is not precisely equivalent to the actual volumetric flow rate, since the method is indirect, e.g. based on the temperature or Coriolis force. It makes the calibration before use mandatory.
Methods of Flow Control
Pressure and flow rate are the main physical parameters which describe flow in microfluidic channels and devices. They are not independent from each other, but related through the flow resistance depending on the channel design and fluid properties quite similar to voltage and current in electrical circuits.
Pressure is defined as force per area and we distinguish hydraulic and pneumatic pressure. These quantities are studied in the fields of Hydraulics and Pneumatics and all together in Hydrodynamics. Hydraulic pressure describes the exerted pressure transmitted by an incompressible medium as a liquid onto an immersed object or a boundary, e. g. water on biological cells or oil phase droplets in multi-phase fluids.
Hydrostatic and Pneumatic Pressure
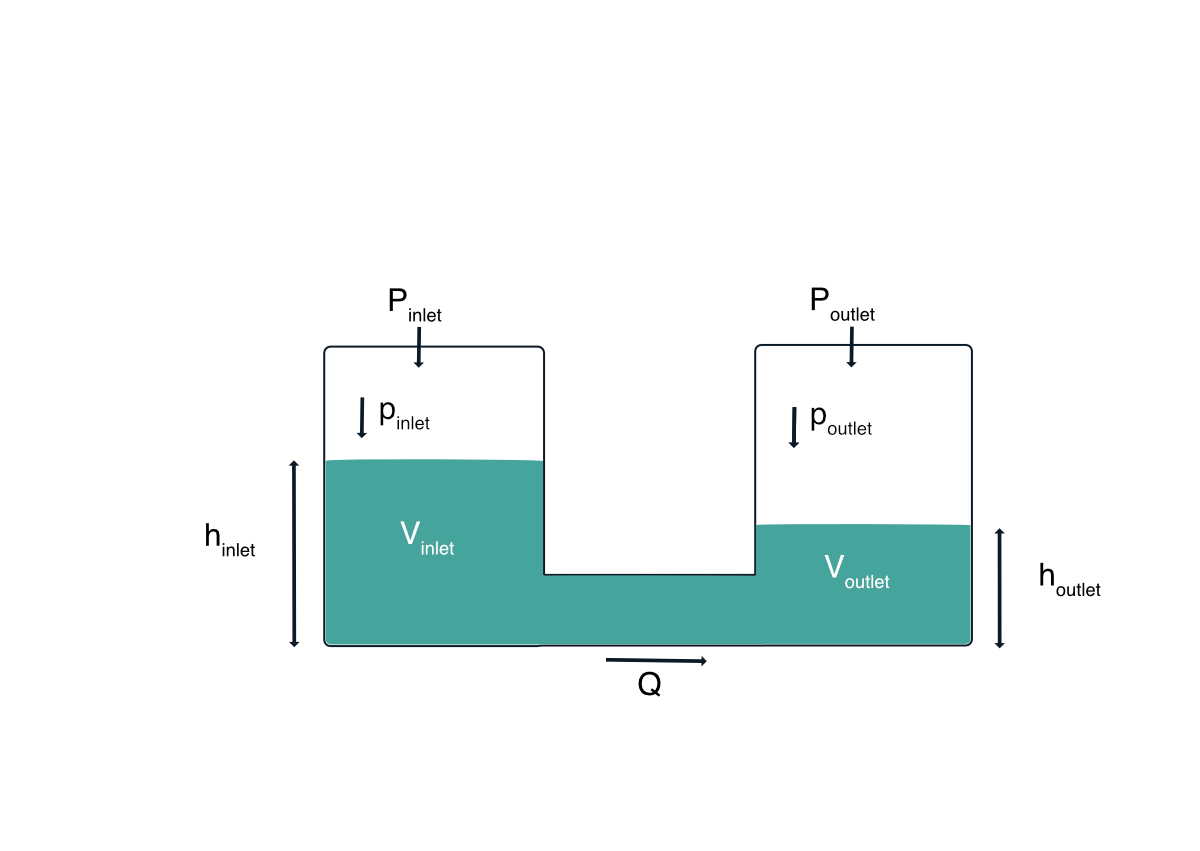
Our atmosphere applies pressure on all surfaces, liquids can also do so. In case of the atmosphere the weight of the entire gas above is pushing downwards due to gravity creating an isotropic pressure to generate a quite impressive pressure at sea level equivalent to approx. a mass of 1 kg pushing on 1 cm2. Liquids, however, have a much higher density than air, approx. 1000-fold, and a much more rapid pressure raise with depth is fact. The pressure of a liquid due to its weight is termed hydrostatic pressure.
The physical origin can be illustrated by a cylinder (or any other shape) placed on a flat surface A. The cylinder with a certain mass and gravitational force F will apply a pressure p onto the bottom interface with given area: p=F / A. This holds true for solid, liquid and gaseous matter as well. When substituting the force term with the material properties of a liquid, e.g. water, and the geometric properties of the hypothetical cylinder, the hydrostatic pressure will be p = h ·ρ · g, whereas h is the height of the liquid column, ρ (“rho”) the liquid density and g the gravitational acceleration. Thus, the hydrostatic pressure does not depend on the size of the cross-sectional area of the liquid column, but only on the height of the liquid column and the density of the liquid. In fact, the hydrostatic pressure is also indifferent to the shape of the hypothetical column.
Newsletter Subscription
We regularly update this page with new technical and application notes as well as background information on Microfluidics, Hydrodynamics and more. If you want to stay updated, please subscribe.